フィルタ挿入によるフランジバックの変化
LRGB合成だけでなく、カラーカメラにおいてもフィルタを使用する機会が増えてきました。私がデュアルナローバンドフィルタを試用させていただいたときにも書いたように、光路中に空気と屈折率の違うフィルタが入ることで、フランジバック(鏡筒やレンズ、補正レンズなどのマウント面からイメージセンサ表面までの距離)は移動します。正しくない位置にイメージセンサを置いた場合、光学系の性能を発揮できない場合があるようです。そこで、今回はフィルタ挿入によるフランジバックの変化がどの程度の量になるのかを計算してみたいと思います。
目次
導出
光路長の変化
Fig. 1は光路中にフィルタがない場合とフィルタが挿入された場合の光路長の変化を示しています。一般的にフィルタに用いられるガラスは空気よりも屈折率が大きいため、フィルタに入射した光線は屈折し、フィルタの外ではふたたび入射光と平行になります。これにより、フィルタ挿入でフランジバックは長くなることになります。この量を\(\Delta f\)とします。今回求めたいフランジバックの変化はこの値となります。まあCADで正しい図を書けば一発なのですが・・・
文字の定義は以下の通りです。
- \(n_0\)・・・空気の屈折率(=1)
- \(n_m\)・・・ガラスの屈折率(ここでは光学ガラスBK7の1.5とした)
- \(\theta_0\)・・・空気中の光の入射角
- \(\theta_m\)・・・フィルタ中の光の屈折角
- \(d\)・・・フィルタの厚み
- \(N\)・・・光学系のF値
- \(f\)・・・光学系の焦点距離
- \(D\)・・・光学系の有効口径
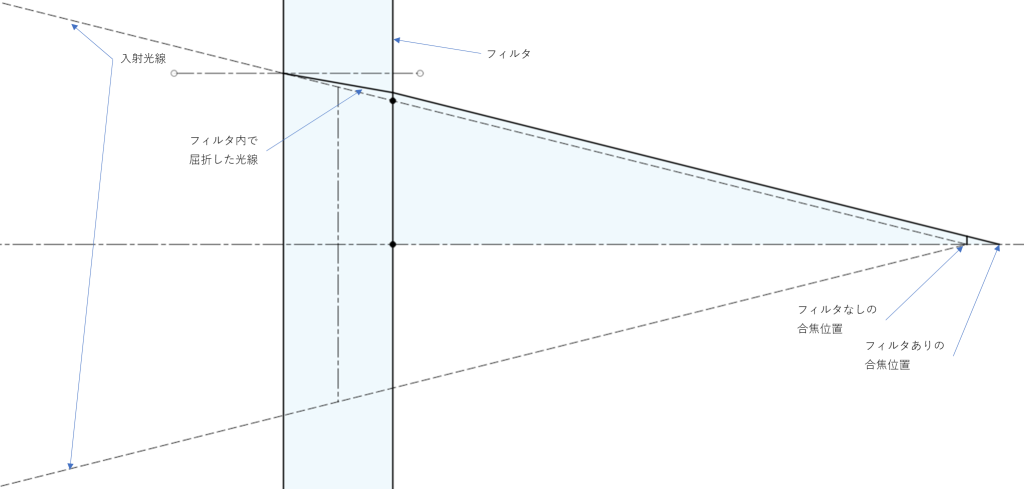
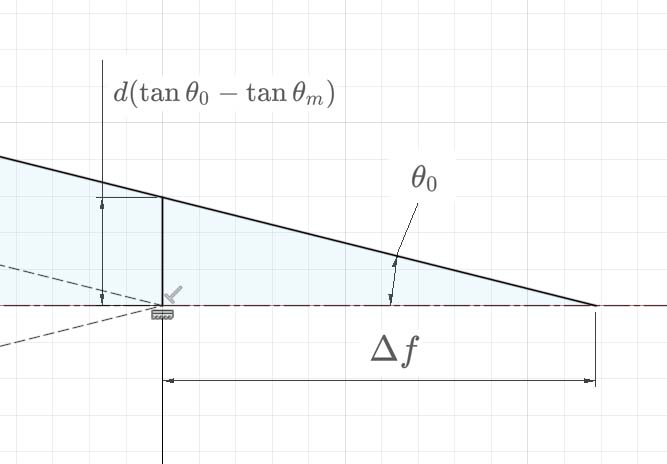
Fig. 2に焦点付近の拡大図を示します。光線の角度は\(\theta_0\)となるので、以下の関係が成り立ちます。
$$
\tan\theta_0 = \frac{d(\tan\theta_0-\tan\theta_m)}{\Delta f}~~~~~~~~~~(1)
$$
よって、
$$
\begin{eqnarray}
\Delta f &=& \frac{d(\tan\theta_0-\tan\theta_m)}{\tan\theta_0} \\
&=& d\left(1-\frac{\tan\theta_m}{\tan\theta_0}\right)~~~~~~~~~~(2)
\end{eqnarray}
$$
を得ます。
\(\theta_0\)の対辺の長さについては、Fig. 3より、フィルタ出口での屈折した光線と屈折しなかった光線のずれ量と等しくなります。
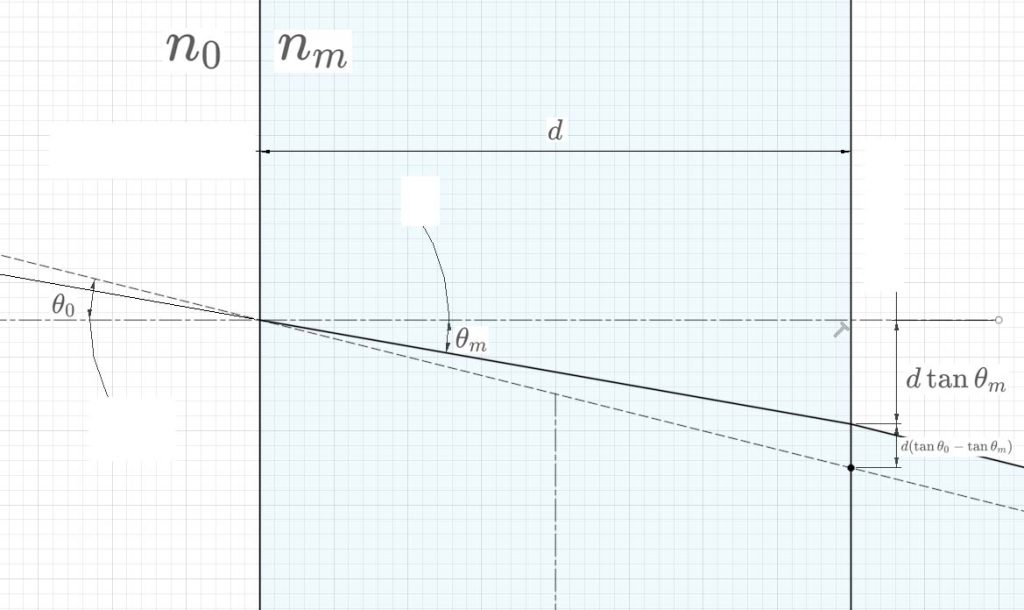
\(\Delta f\)の厳密解
次に、(2)式より、\(\theta_0\), \(\theta_m\)を消去して、光学系のパラメータに置き換えます。\(\theta_0\)については、光学系のF値の定義(Fig. 4参照)から、次の関係が成り立ちます。
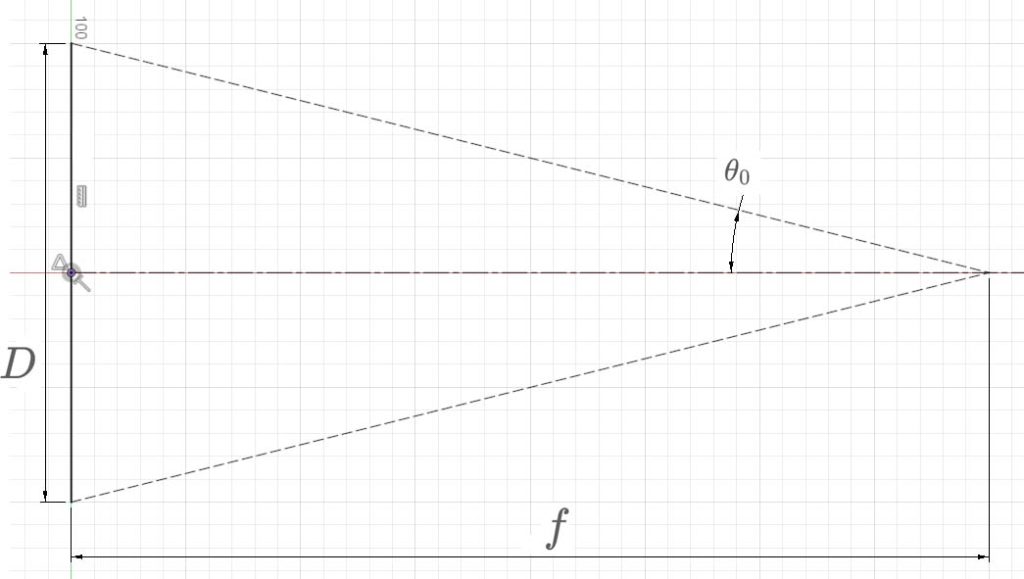
$$
\tan\theta_0 = \frac{D}{2f}~~~~~~~~~~(3)
$$
\(N=\frac{f}{d}\)より、
$$
\theta_0 = \arctan\left (\frac{1}{2N}\right)~~~~~~~~~~(4)
$$
\(\theta_m\)については、スネルの法則より
$$
\frac{\sin\theta_m}{\sin\theta_0} = \frac{n_0}{n_m}~~~~~~~~~~(5)
$$
よって、
$$
\theta_m = \arcsin\left(\frac{n_0}{n_m}\sin\theta_0\right)~~~~~~~~~~(6)
$$
(2)式に(5)式を代入して、\(\theta_m\)を消去します。\(\cos\theta = \sqrt{1-\sin^2\theta}~~( 0^{\circ}<\theta<90^{\circ})\)を利用すると、
$$
\begin{eqnarray}
\Delta f &=& d\left(1-\frac{\tan\theta_m}{\tan\theta_0}\right) \\
&=& d\left(1-\frac{\sin\theta_m}{\sin\theta_0}\sqrt{\frac{1-\sin^2\theta_0}{1-\sin^2\theta_m}}\right) \\
&=&d\left(1-\frac{n_0}{n_m}\sqrt{\frac{1-\sin^2\theta_0}{1-\left(\frac{n_0}{n_m}\sin\theta_0\right)^2}}\right)~~~~~~~~~~(7)
\end{eqnarray}
$$
を得ます。(4)式を(7)式に代入すると、\(\Delta f\)の厳密解が得られます(式が煩雑になるので省略します)。(7)式より、\(\Delta f\)は\(d, ~n_0,~ n_m,~ N\)の関数であることがわかります。つまり、フィルタ挿入によるフランジバックの変化は、フィルタの板厚、フィルタの屈折率、光学系のF値のみによって決まることがわかります。そのため、フィルタの挿入位置には依存せず、フィルタはどこに入れてもフランジバックは変わらず、合焦位置も変化しないことになります。(ただし、フィルタをイメージセンサ面から遠ざけた場合、フィルタ枠によるケラレが発生します。また、フィルタとセンサの間で往復反射が起こり、ゴーストが発生する可能性があります。)
※ところで、(7)式を積分すると、第二種完全楕円積分の形になりますね。初めて超越関数に出会った時のワクワクを思い出します。
\(\Delta f\)の近似解
F値 \(N\)が十分に大きい場合、(4)式より\(\theta_0\)は0に近づきますから、\(\theta_0\approx \tan\theta_0\approx\sin\theta_0\)の近似が成り立ちます。よって、(2)式は次のように近似できます。
$$
\begin{eqnarray}
\Delta f’ &=& d\left(1-\frac{\tan\theta_m}{\tan\theta_0}\right) \\
&\approx& d\left(1-\theta_0\frac{n_0}{n_m}\cdot \frac{1}{\theta_0}\right) \\
&=&d\left(1-\frac{n_0}{n_m}\right)~~~~~~~~~~(8)
\end{eqnarray}
$$
この(8)式が、一般にフィルタによるフランジバックの変化を求める式としてよく紹介されていると思います。より簡便に、BK7の屈折率1.5を代入して、\(\Delta f \approx \frac{d}{3}\)としている文脈もよく見かけます。この式では、フランジバックの変化はフィルタの板厚と屈折率のみで決まります。さて、実際に撮影で使用している光学系において、この近似は妥当なのでしょうか?次に、実際の撮影を想定したパラメータを代入して、厳密解と近似解の誤差を検証します。
厳密解と近似解の誤差
厳密解と近似解の誤差を求めるため、(7) 式と(8)式より、\(\Delta f-\Delta f’\)を計算してみます。計算にあたっては、F値以外のパラメータは以下としました。
- \(n_0\)=1.0
- \(n_m\)=1.5
- \(d\)=2.0
両者の差は、光学系のF値がパラメータに含まれるかどうかです。F値が大きくなるほど、両者のずれは小さくなるはずです。
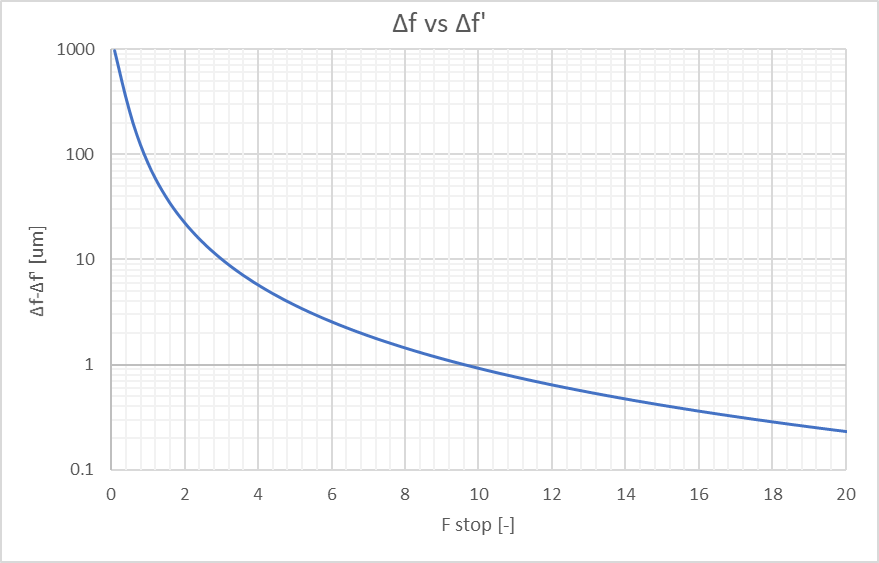
Fig. 5に結果を示します。上述の通り、F値が大きくなるほど\(\Delta f\)と\(\Delta f’\)のずれは小さくなります。一般的に、天体写真の撮影に使用される光学系のF値はF1.8-F8.0程度でしょう。F1.8ではずれが約20 umとなります。このずれを許容するかどうかは人によって意見が分かれそうですが、私としては20 umのずれはシムリングで補正可能なので、補正したいところです。逆に、10 umを下回るような差を調整するのは困難です。また、このくらいの量は温度変化による膨張収縮で簡単に動いてしまいます。以上の理由から、\(\Delta f-\Delta f’\)の値が10 umを切ってくるF3.0前後を境に、厳密解と近似解を使い分けるのが良さそうです。また、F8以上であれば近似解を適用しても良いだろうとする見解もありました。(もっとも、厳密解についてもエクセルの数値計算で簡単にできるので、個人的には常に厳密解を使用したいです。)
まとめ
フィルタ挿入によるフランジバックの変化は次の式で表されることがわかりました。
$$
\Delta f =d\left(1-\frac{n_0}{n_m}\sqrt{\frac{1-\sin^2\theta_0}{1-\left(\frac{n_0}{n_m}\sin\theta_0\right)^2}}\right) \\
\mathrm{where} ~~~\theta_0 = \arctan\left (\frac{1}{2N}\right)
$$
ただし、F値が十分に大きい場合は
$$
\Delta f’ = d\left(1-\frac{n_0}{n_m}\right)
$$
基本的には数値計算で\(\Delta f\)の厳密解を計算する。という運用で行きたいと思います。
実際に、フランジバックの量と星像の乱れを実写で検証してみたいです。・・・続く?